BIOGRAFIAS

-


 TALES DE MILETO:


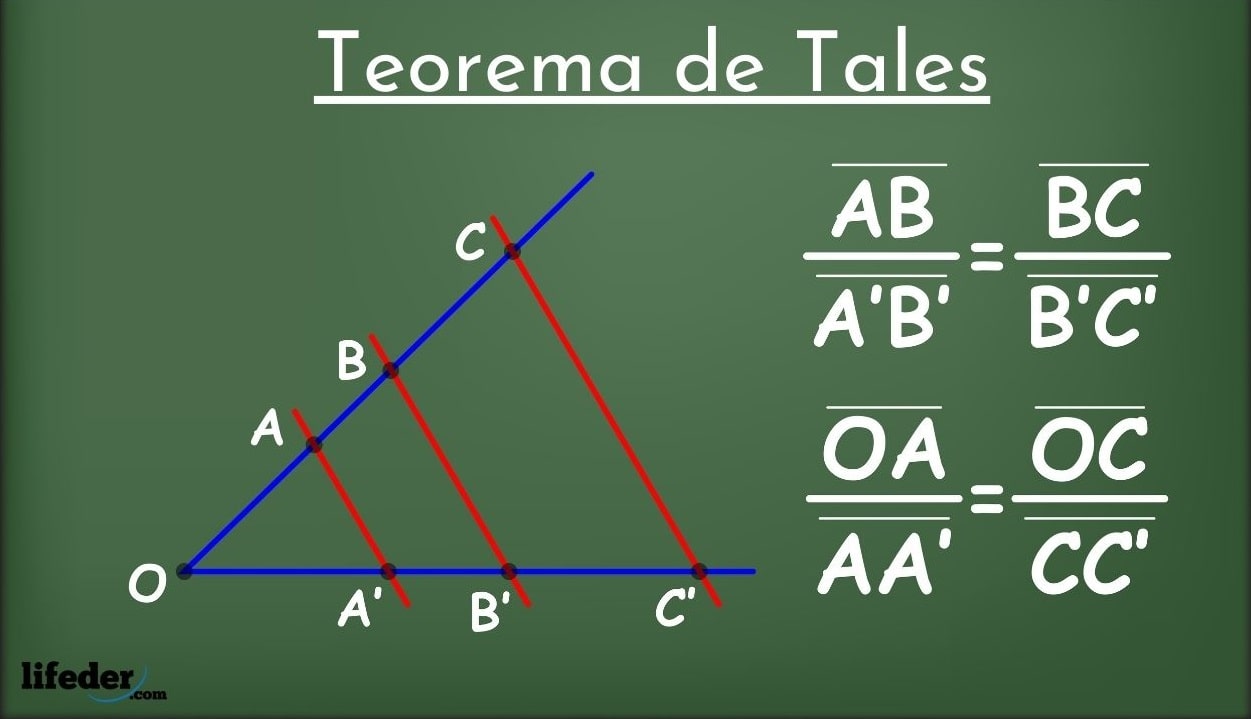
https://fotos.perfil.com/2019/05/21/trim/987/555/tales-de-mileto-705068.jpg?webp

 Tales de Mileto, además de ser un destacado filósofo y matemático, fue un pensador versátil con intereses que abarcaban la astronomía, la geometría y la física. Su teorema más conocido, el Teorema de Tales, establece que, si trazamos dos líneas paralelas y dibujas segmentos de línea desde un punto exterior hasta las líneas paralelas, estos segmentos cortarán las líneas en puntos que están en proporciones iguales. Este teorema es fundamental en la geometría y ha sido utilizado en diversos campos, desde la trigonometría hasta la teoría de números.

Tales también se destacó por su capacidad para aplicar conceptos matemáticos en la predicción de eventos astronómicos, como el eclipse solar que predijo en el año 585 a.C. Aunque sus métodos exactos no están documentados, su capacidad para relacionar la matemática con fenómenos naturales refleja una mentalidad científica y analítica única para su época.

TEOREMA DE THALES 



 Imagen Teorema de tales de mileto (S.F.) lifeder. (jpg). https://www.lifeder.com/teorema-tales-mileto/

La declaración formal del Teorema de Tales es la siguiente:

En un triángulo, si trazas líneas paralelas a uno de los lados, dividen los otros dos lados en segmentos proporcionales.

Para expresarlo de manera más clara, considera un triángulo ABC. Si trazas una línea paralela a un lado del triángulo (por ejemplo, el lado BC), interceptando los otros dos lados (AB y AC), entonces los segmentos de esos dos lados creados por la línea paralela son proporcionales a los lados originales.

En términos matemáticos, si la línea paralela corta AB en D y AC en E, y si F es el punto de intersección de BC y DE, entonces:

 Imagen Teorema de tales de mileto (S.F.) relación de proporcionalidad. lifeder. (jpg). https://www.lifeder.com/teorema-tales-mileto/

Este teorema es aplicable no solo a triángulos, sino también a situaciones más generales, como segmentos cortados por líneas paralelas en figuras geométricas.

El Teorema de Tales es fundamental en geometría y tiene diversas aplicaciones, incluyendo la resolución de problemas de proporciones en triangulación, así como en la trigonometría y la teoría de números. Es un concepto esencial que se enseña en los primeros niveles de educación matemática y sigue siendo relevante en estudios más avanzados.

ZENÓN DE ELEA:

 

Imagen Zenon de elea. (s.f.) Imagen (jpg) Dreamstime. url: https://es.dreamstime.com/foto-de-archivo-zenon-de-elea-zeno-muri%C3%B3-cerca-de-antes-de-que-cristo-aislara-el-marb-image42743133

Zenón, por otro lado, se centró más en la filosofía y la lógica, presentando paradojas que desafiaban la comprensión común del movimiento y el infinito. Sus paradojas, como la mencionada "paradoja de Aquiles y la tortuga", apuntaban a demostrar que el movimiento era una ilusión y que el espacio y el tiempo podían dividirse infinitamente, lo que planteaba preguntas profundas sobre la naturaleza de la realidad.

Su contribución al estudio del infinito y su defensa del pensamiento abstracto influyeron significativamente en filósofos y matemáticos posteriores, como los fundadores del cálculo en el siglo XVII. Aunque algunas de sus paradojas fueron resueltas con el tiempo, su trabajo generó un debate duradero sobre conceptos fundamentales y cuestiones metafísicas relacionadas con el espacio y el tiempo.

 IMAGEN La tortuga combate a Aquiles. (sf). Cuaderno de cultura científica. (jpg). https://es.dreamstime.com/foto-de-archivo-zenon-de-elea-zeno-muri%C3%B3-cerca-de-antes-de-que-cristo-aislara-el-marb-image42743133

En la paradoja de Aquiles y la tortuga, Zenón propone una situación hipotética en la que Aquiles, el héroe griego, se enfrenta a una tortuga en una carrera. Aunque Aquiles es mucho más rápido que la tortuga, Zenón argumenta que Aquiles nunca alcanzará a la tortuga si ésta comienza con una pequeña ventaja.

El razonamiento detrás de la paradoja implica dividir la distancia entre Aquiles y la tortuga en una serie infinita de pasos más pequeños. Cada vez que Aquiles alcanza el lugar donde estaba la tortuga, la tortuga ya ha avanzado un poco. Este proceso se repite infinitamente, y según Zenón, Aquiles nunca superará completamente la ventaja inicial de la tortuga.

La paradoja de Zenón destaca la paradoja aparente de sumar una serie infinita de términos, ya que, en teoría, Aquiles debería ser capaz de alcanzar a la tortuga. Sin embargo, estas paradojas se resuelven en la teoría matemática moderna mediante el uso de conceptos como el límite y la convergencia infinita. La paradoja de Zenón juega un papel importante en la comprensión de la teoría matemática y ha llevado a desarrollos en el análisis matemático y la teoría de conjuntos.

Generalidades y curiosidades

Tales vs Zenon

Tales de Mileto (c. 624-546 a.C.):

Orígenes y ocupaciones múltiples: Tales fue un filósofo, matemático y astrónomo griego. Provenía de Mileto, una antigua ciudad griega en Asia Menor (actual Turquía).

Predicciones astutas: Se le atribuye la predicción de un eclipse solar en el año 585 a.C., lo que muestra su interés en la astronomía. Algunos historiadores consideran este evento como el primer uso registrado de la razón y la observación para prever un fenómeno natural.

Foco en lo práctico: Aunque se le considera uno de los Siete Sabios de Grecia y un pensador presocrático, Tales también estaba interesado en cuestiones prácticas, como la ingeniería. Se le atribuyen mejoras en la navegación y en la agricultura.

Elemento fundamental: Tales es famoso por postular que el agua es el principio básico de todas las cosas. Creía que todo estaba compuesto de agua en diferentes formas y estados.

Zenón de Elea (c. 490-430 a.C.):

Discípulo de Parménides: Zenón fue discípulo de Parménides, otro influyente filósofo presocrático. Parménides sostenía que el cambio y el movimiento eran ilusiones, y Zenón desarrolló paradojas para respaldar esta idea.

Paradojas famosas: Zenón es conocido por sus paradojas, como la paradoja de Aquiles y la tortuga, que plantea la idea de que el movimiento es imposible debido a infinitos pasos que deben completarse.

Defensor de la filosofía de Parménides: Aunque las paradojas de Zenón fueron diseñadas para respaldar las ideas de su maestro Parménides, también generaron debates y desafíos para los filósofos posteriores que intentaron resolverlas.

Influencia en la matemática: A pesar de su enfoque en la filosofía, las paradojas de Zenón también tuvieron un impacto en la matemática. La noción de infinitesimales y la convergencia de series infinitas son temas que se relacionan con sus paradojas.

Paralelos entre Tales y Zenón:

Orígenes geográficos: Ambos eran originarios de regiones cercanas de la antigua Grecia, con Tales proveniente de Mileto y Zenón de Elea.

Influencia en la filosofía presocrática: Tales y Zenón fueron figuras clave en el desarrollo de la filosofía presocrática, que buscaba explicar la naturaleza fundamental del mundo y sus principios básicos.

Interés en la naturaleza y la realidad: Ambos filósofos compartían un interés en comprender la realidad y la naturaleza fundamental de las cosas, aunque abordaban estos temas desde perspectivas diferentes.

En resumen, la Comparación de sus aportes matemáticos: La contribución de Tales se centra en la aplicación práctica de la matemática a través de la geometría, proporcionando teoremas y principios que se utilizan hasta el día de hoy. Por otro lado, Zenón desafiaba los fundamentos mismos de las matemáticas al explorar la naturaleza del infinito y la realidad del movimiento. Mientras que Tales se destacó por sus contribuciones prácticas, Zenón influenció el desarrollo de la teoría matemática y filosófica.

Tales de Mileto fue un pionero en la aplicación práctica de las matemáticas, especialmente en geometría y astronomía, mientras que Zenón de Elea fue un provocador intelectual que desafió las percepciones convencionales a través de sus paradojas, influyendo en la evolución del pensamiento matemático y filosófico. Ambos dejaron un legado duradero en sus respectivos campos.

Bibliografía:

Tales de Mileto:

Jaeger, W. (1986). La teología de los primeros filósofos griegos. Fondo de Cultura Económica.

Kirk, G. S., Raven, J. E., & Schofield, M. (1994). Los filósofos presocráticos. Gredos.

Zenón de Elea:

Aristóteles. (2006). Física. Gredos.

Diels, H., & Kranz, W. (2009). Los fragmentos de los presocráticos. Gredos.

 ARQUÍMEDES

Foto: Arquímedes / Domenico Fetti [Public domain], via Wikimedia Commons

Arquímedes nació en Siracusa, Sicilia, en el año 287 a.C. y falleció en 212 a. C durante la Segunda Guerra Púnica. De lo poco que se conoce de Arquímedes se cree que es hijo de Fidia, un famoso astrónomo y matemático de la época, quien posiblemente fue el creador de la pasión por la ciencia en Arquímedes.

Debido a la poca información sobre su nivel de estudio, se cree que estudió en la escuela del matemático Euclides en Alejandría, Egipto. Se desconoce exactamente qué estudio, pero sus conocimientos fueron fortalecidos en matemáticas y física, parte fundamental de sus constantes investigación y experimentos.

Arquímedes se destacó en los estudios, experimentos e investigaciones de diferentes temas de las matemáticas y la física. Como uno de sus aportes principales encontramos el teorema de Arquímedes, este teorema nación cuando tomaba un baño, en el proceso visualizo que el nivel del agua en la tina subía cuando él entraba, este evento lo llevó a determinar el volumen de la corona. Este principio también es conocido como el principio de Hidrostática, el fin del mismo es que todo cuerpo sumergido en el fluido experimenta un empuje vertical y hacia arriba igual al peso del volumen del fluido desalojado ( , donde E es el empuje, Pe es el peso específico (N/m³), V es el volumen de fluido desplazado por un cuerpo sumergido en él, g es la aceleración de la gravedad.

Otro de sus aportes es el cálculo del área de una parábola, utilizó el método de la exhaución (aproximación al perímetro o al área de figuras curvas), bajo la utilización de este método se determinó el área bajo el arco de una parábola con el sumatorio de una serie infinita ( . También fue uno de los investigadores que se aproximó a la medida precisa del número pi (π).

Fue el que desarrolló métodos para calcular el volumen de las figuras como la esfera, el cilindro y el cono, utilizando el método de agotamiento que consiste en dividir una figura en finito de piezas y luego calcular el volumen sumando los volúmenes de las piezas. En la geometría formuló teoremas sobre el centro de gravedad de figuras planas y sólidos.

En lo que respecta a la física, Arquímedes realizó aportes significativos en lo referente al principio de la palanca, concluyendo en la explicación de su funcionamiento y sus tipos, además de aportes al diseño de máquinas como la catapulta, la pole compuesta, los espejos cóncavos y el tornillo de Arquímedes. Sentó bases en la hidrostática y estudios en la refracción de la luz y la reflexión.

Fue considerado como uno de los científicos más importante de la época, con sus descubrimientos e inventos generó impactos en la ciencia y la tecnología, y continúa siendo un referente para los científicos y en la ingeniería actualmente.

GALILEO GALILEI

 

(Volumen de la esfera y el misterio de la tumba de Arquímedes, 2020)https://images.app.goo.gl/2ZHA86Bg3eadWJkEA

Nació el 15 de febrero de 1564 en Pisa, Italia. Sus familiares eran comerciantes. Su educación inicial fue recibida en casa hasta la edad de 10 años. Luego ello junto a sus padres se trasladó a Florencia Italia, debido a las obligaciones de sus padres, fue dejado a cargo de un vecino, quien infundió pensamiento religiosos y lo matriculó en un convento. Su padre no permitió que continuara en el convento. Inició sus estudios de medicina en 1581 en la universidad de Pisa, pero no encontró vocación en esta carrera, abandonando los estudios universitarios a sus 21 años. De este paso por la medicina creció su interés por las matemáticas, encontrando la vocación en la Física.

En su proceso de estudio de Física, se destacó en la universidad por los experimentos en mecánica, permitiéndole ganar reputación y prestigio, cosa que lo llevó a ser aceptado como profesor de matemáticas en la misma universidad. Luego de su traslado a Padua desempeñó sus labores como profesor de Astronomía, mecánica y Geometría en una universidad de allí.  Fue censurado por la iglesia por sus investigaciones, pues ellos iban en contra de los pilares y creencias de la iglesia. Le fue prohibido difundir la teoría heliocéntrica. Continuó sus investigación y experimentos desde su residencia, de manera incógnita, pero al cabo de unos años publicó una obra llamada “Diálogos sobre los dos máximos sistemas del mundo. Esto genero que la iglesia investigara, fuera retenido y fue obligado a confesar su delito por las amenazas de tortura que recibió. Rechazó sus ideas y fue recluido en su casa.

Al cabo de algunos años luego de quedar ciego se trasladó a otro Domicilio cerca del mar y finalmente falleció a la edad de los 77 años en Arcetri el 8 de enero de 1642.

Galileo, realizó aportes significativos a las matemáticas, astronomía y física. Se pueden identificar experimentos, investigaciones y de ellos la generación de teorías que hoy en día son importantes y utilizadas de manera constante.

En lo referente a la geométrica y las matemáticas, Galileo, aportó en temas como: la invención del compás o pantómetra, que son dos regletas graduadas; realizó aportes en la geometría proyectiva mediante el estudio de la perspectiva de los objetos tridimensionales en un plano bidimensional, el estudio de las proyecciones de figuras geométricas, la aplicación de las proyecciones en la astronomía para calcular la distancia a las estrellas. También aportó en el estudio del movimiento por medio de experimentos y mediciones, descubriendo la caída libre de los objetos y el movimiento de los proyectiles, aporte significativo para la mecánica clásica. Además, aplicó las matemáticas en la física para la formulación de leyes físicas y cuantificables.

Aportó en la invención del telescopio, descubriendo por medio de él las fases de venus, los cuatro satélites más grandes de Júpiter y las manchas solares, invención del termoscopio que media la temperatura, precursor del termómetro, entre otros que hoy en día son utilizados en la ciencia, las matemáticas, la astronomía, la física.

Bibliografía

buscabiografia. (s.f.). Obtenido de https://www.buscabiografias.com/biografia/verDetalle/2452/Arquimedes


Fundación Aquae. (25 de noviembre de 2020). Obtenido de https://www.fundacionaquae.org/principio-arquimedes-eureka/


historia.nationalgeographic.com.es. (08 de 01 de 2021). Obtenido de https://historia.nationalgeographic.com.es/a/galileo-astronomo-mas-persistente_16083


Wikipedia. (27 de febrero de 2024). Obtenido de https://es.wikipedia.org/wiki/Principio_de_Arqu%C3%ADmedes


Wikipedia. (07 de 04 de 2024). Obtenido de https://es.wikipedia.org/wiki/Galileo_Galilei


Wikipedia. (25 de 02 de 2024). Obtenido de https://es.wikipedia.org/wiki/Geometr%C3%ADa_proyectiva


YouTube. (26 de 07 de 2020). Obtenido de https://www.youtube.com/watch?v=XO-ZYtTrJPg

RENE DESCARTES

 Fuente: https://www.buscabiografias.com/img/people/Descartes.jpg

Biografía:

René Descartes (1596-1650) fue un filósofo, matemático y científico francés, considerado el padre de la filosofía moderna, la geometría analítica y el mecanicismo en la física. Nació en La Haye en Touraine, Francia, y recibió una educación jesuítica de élite, donde se destacó en las matemáticas y la filosofía. Tras completar sus estudios, viajó por Europa, absorbiendo las ideas de diversas corrientes intelectuales.

En 1619, Descartes experimentó una epifanía mientras se encontraba acuartelado en Breda, Holanda. Convencido de la necesidad de un método racional para alcanzar el conocimiento verdadero, se dedicó a desarrollar su propio sistema filosófico, plasmado en su obra más famosa, "Discurso del Método" (1637).

Descartes es reconocido por su célebre frase "Pienso, luego existo" ("Cogito, ergo sum"), que resume su búsqueda de un fundamento seguro para el conocimiento. Propuso un método basado en la duda metódica, cuestionando todo aquello que pudiera ser puesto en duda, hasta llegar a verdades indubitables.

Aportes al Álgebra y la Geometría:

Descartes realizó importantes contribuciones al álgebra y la geometría, sentando las bases para la geometría analítica. Su obra "La Geometría" (1637) introdujo un sistema de coordenadas, conocido como sistema cartesiano, que permite representar figuras geométricas mediante ecuaciones algebraicas y viceversa. Esta innovación revolucionó las matemáticas, permitiendo la traducción de problemas geométricos en problemas algebraicos y viceversa, facilitando su resolución.

Obras notables:

  • Discurso del Método (1637)
  • Meditaciones sobre la Filosofía Primera (1641)
  • Principios de la Filosofía (1644)
  • La Geometría (1637)

Fuentes:

Isaac Newton:

Fuente: https://museovirtual.csic.es/salas/luz/img/Sir_Isaac_Newton_(1643-1727).jpg

Biografía:

Isaac Newton (1643-1727) fue un físico y matemático inglés, considerado uno de los científicos más influyentes de todos los tiempos. Nació en Woolsthorpe, Inglaterra, y estudió en el Trinity College de la Universidad de Cambridge, donde se destacó por su talento en las matemáticas y la física. Tras graduarse, se dedicó a la investigación científica, realizando importantes descubrimientos en diversas áreas.

Aportes a la Matemática y la Física:

Newton es reconocido por sus tres leyes del movimiento y su ley de gravitación universal, que sentaron las bases de la mecánica clásica. Sus leyes del movimiento describen el comportamiento de los objetos en movimiento, mientras que su ley de gravitación universal explica la fuerza de atracción entre dos objetos con masa. Estos descubrimientos revolucionaron nuestra comprensión del universo y sentaron las bases para la física moderna.

Además de sus contribuciones a la física, Newton realizó importantes aportes a las matemáticas, incluyendo el desarrollo del cálculo infinitesimal. El cálculo es una herramienta matemática esencial para el estudio del movimiento, el cambio y las curvas, y ha tenido un impacto profundo en diversas áreas de la ciencia y la ingeniería.

Obras notables:

  • Philosophiæ Naturalis Principia Mathematica (Principios Matemáticos de la Filosofía Natural) (1687)
  • Opticks (Óptica) (1704)
  • Methodus Fluxionum et Serierum Infinitarum (Método de las Fluxionesy Series Infinitas) (1736)

Fuentes:

Conclusión:

René Descartes e Isaac Newton fueron figuras intelectuales de gran trascendencia, cuyas contribuciones a las matemáticas, la física y la filosofía han tenido un impacto profundo en el desarrollo del conocimiento humano. Sus ideas sentaron las bases para la ciencia moderna y continúan inspirando a científicos e investigadores de todo el mundo.


Explores the history of mathematics from antiquity to the contemporary era, highlighting the key contributions of René Descartes and Isaac Newton. It analyzes how mathematics has evolved over time, from the numerical systems of antiquity to modern developments in algebra, geometry, and calculus. The role of Descartes in introducing analytic geometry, which united algebra and geometry, laying the groundwork for modern calculus, is emphasized. Additionally, Newton's contributions to physics and mathematics are examined, including his laws of motion and the law of universal gravitation, which revolutionized our understanding of the universe.
1, 2, 3, 4, 5, 6

Comentarios

Publicar un comentario